2.4. Системы случайных величин

Во многих задачах приходится рассматривать одновременно две или более случайные величины. Возникающую при этом систему из конечного числа случайных величин назовём – мерной случайной величиной. Заказывая партию костюмов, торговая фирма должна иметь некоторую информацию о распределении у потенциальных покупателей хотя бы двух случайных параметров – размера и роста.

В дальнейшем мы ограничимся рассмотрением двумерной случайной величины. При сохранении главного упрощаются выкладки и появляется возможность дать геометрическую интерпретацию.

В дискретном случае возможные значения двумерной случайной величины можно рассматривать как координаты случайной точки на плоскости – . Чтобы задать случайную величину, в этом случае надо указать перечень возможных значений и вероятности того, что компоненты и примут значения и . Как и в одномерном случае это можно сделать в виде таблицы (но уже с двумя входами) или аналитически (некоторой формулой):

		…
		…
…	…	…	…
		…

Поскольку события, заключающиеся в том, что и при несовпадении хотя бы одного индекса несовместны, а их сумма – достоверное событие, то

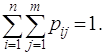(2.39)

Для описания непрерывной двумерной случайной величины , как и в одномерном случае, введём понятие функции распределения

(2.40)

Рис.2.11

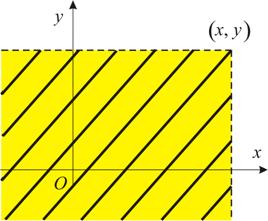
Таким образом, значение функции распрделения в точке равно вероятности того, что случайная точка с координатами попадёт в квадрант с вершиной в точке , изображённый на Рис.2.11.

Как и в одномерном случае, функция распределения двумерной случайной величины обладает рядом свойств:

1. (2.41)

2. – функция, не убывающая по каждому аргументу.

3. (2.42)

4. Обозначим функции распределения компонент и двумерной случайной величины соответственно и , тогда

(2.43)

5. Вероятность попадания случайной точки в прямоугольник равна

(2.44)

Предположим теперь, что функция распределения имеет смешанную частную производную второго порядка, которую назовём плотностью вероятности двумерной случайной величины:

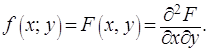(2.45)

Как и в одномерном случае, плотность вероятности двумерной случайной величины обладает рядом свойств:

1. (2.46)

2.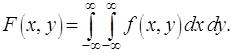 (2.47)

Следствие:

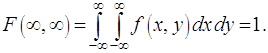(2.48)

3. потому называется плотностью вероятностей двумерной величины, что как и в одномерном случае, она равна отношению вероятностей попадания случайной точки в некоторую область, содержащую точку , к её площади, при неограниченном уменьшении её размеров.

4. Вероятность попадания случайной величины в заданную область

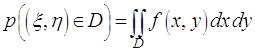(2.49)

5. Плотности вероятностей и компонент и определяются по плотности вероятности двумерной случайной величины следующим образом

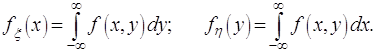(2.50)

Зависимость случайных величин

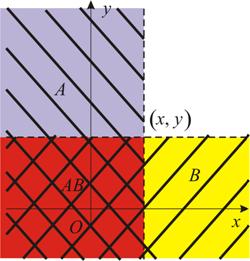
Рассмотрим двумерную случайную величину , заданную плотностью вероятности , по которой при необходимости может быть найдена функция распределения . Обозначим попадание случайной точки в полуплоскость событием , в полуплоскость событием (Рис.2.12). Тогда значение функции распределения – вероятность попадания случайной точки в квадрант будет равно вероятности произведения событий и , то есть

Рис.2.12

Учитывая, что функция распределения компонент есть

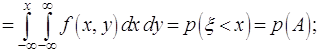
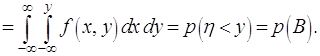
Примем за основу определение независимости случайных событий и назовём компоненты двумерной случайной величины и независимыми, если

Откуда:

(2.51)

то есть

назовём компоненты двумерной случайной величины независимыми, если её функция распределения равна произведению функций распределения компонент.

Аналогичное утверждение справедливо и для плотностей вероятности

(2.52)

Следствие. Если случайные величины и независимы, то по известным распределениям компонент и можно восстановить распределение системы .