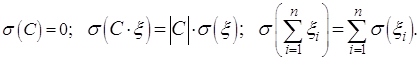2.2. Числовые характеристики случайной величины

Случайная величина полностью определяется её законом распределения, но для многих задач эта информация излишне полна и в то же время на практике часто закон распределения не известен и приходится довольствоваться меньшими сведениями. В таких случаях пользуются некоторыми суммарными характеристиками случайной величины. К важнейшим из них относятся математическое ожидание и дисперсия.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех её возможных значений на их вероятности:

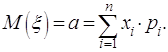(2.13)

Математическим ожиданием непрерывной случайной величины называется интеграл:

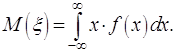(2.14)

Подчеркнём, что математическое ожидание случайной величины есть некоторое число (постоянная, неслучайная величина).

Пример 6.

Закон распределения случайной величины задан таблично (найден в примере 1). Найти математическое ожидание.

	0	1	2
	0.08	0.44	0.48

Решение. По определению:

Пример 7.

Задана плотность вероятности случайной величины (найдена в примере 4). Найти математическое ожидание.

Решение. Разобьём интеграл по всей оси на три интеграла. Учитывая, что на двух интервалах интегрирования плотность вероятности равна нулю, по определению получаем:

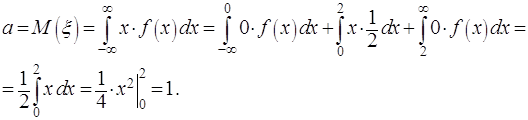
Для понимания очень полезна механическая аналогия. Трактуя возможные значения случайной величины как координаты точек на оси, а соответствующие им вероятности – как некоторые (вероятностные) массы, можно заметить, что математическое ожидание является аналогом понятия центра масс, то есть является тем «средним», «центральным» значением,

Свойства математического ожидания

Математическое ожидание постоянной равно самой постоянной

(2.15)

Действительно, Постоянную можно рассматривать как дискретную случайную величину, принимающую единственное значение с вероятностью 1, поэтому

Постоянный множитель можно выносить за знак математического ожидания

(2.16)

Поскольку при умножении на возможные значения случайной величины также умножаются на , при сохранении соответствующих вероятностей, то (2.16) следует из известных свойств суммы и интеграла.

Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий слагаемых

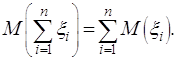(2.17)

Математическое ожидание произведения конечного числа независимых в совокупности случайных величин равно произведению математических ожиданий сомножителей

(2.18)

Итак, математическое ожидание является тем «средним» значением, вокруг которого распределены все возможные значения случайной величины. Однако, знания среднего значения случайной величины для большинства задач недостаточно, необходимо иметь ещё количественную характеристику разброса возможных значений случайной величины относительно математического ожидания. Для этого рассмотрим разность – отклонение возможного значения случайной величины от её математического ожидания:

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

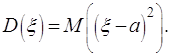(2.19)

Для вычисления дисперсии часто оказывается полезной формула:

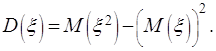(2.20)

Действительно:

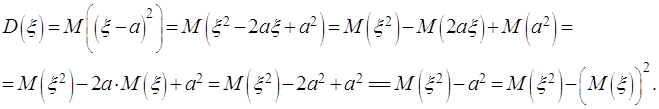
Свойства дисперсии

Дисперсия постоянной равна нулю

(2.21)

Действительно,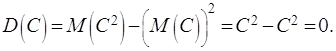

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

(2.22)

Действительно,

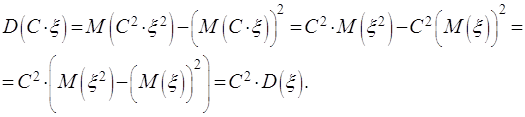
Дисперсия суммы (разности) конечного числа независимых в совокупности случайных величин равна сумме дисперсий слагаемых:

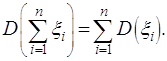(2.23)

Действительно,

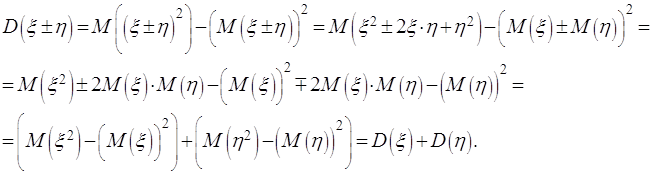
Поскольку размерность дисперсии случайной величины равна квадрату размерности самой случайной величины, то в ряде случаев удобнее пользоваться корнем из дисперсии. Эта характеристика имеет ту же размерность, что и сама случайная величина, и её называют среднеквадратическим отклонением.

(2.24)

Из свойств дисперсии следуют свойства среднеквадратического отклонения: