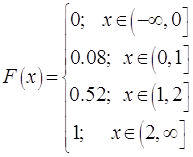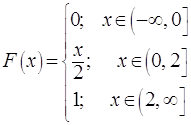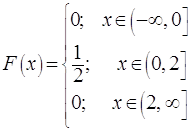2.1.
Основные понятия
Наряду со
случайными событиями одним из основных понятий теории вероятностей является
понятие случайной величины.
Случайной называется величина, численное значение которой
может меняться в зависимости от результата стохастического эксперимента
Примерами
случайных величин могут быть отметка на экзамене – целое положительное число
(от 2 до 5), число оборотов спутника вокруг Земли до его гибели – любое целое
неотрицательное число (в принципе, ничем не ограниченное), продолжительность
работы телевизора до выхода из строя – любое неотрицательное число и т.д.
Обозначать
случайные величины будем греческими буквами ![]() и т.д., а их
возможные значения –
и т.д., а их
возможные значения – ![]() , снабжая их при необходимости индексами.
, снабжая их при необходимости индексами.
Таким
образом, случайная величина ![]() – число, которое ставится в соответствие
каждому возможному исходу стохастического эксперимента. Поскольку исходы опыта
полностью определяются элементарными событиями, можно рассматривать случайную
величину как функцию от элементарного события
– число, которое ставится в соответствие
каждому возможному исходу стохастического эксперимента. Поскольку исходы опыта
полностью определяются элементарными событиями, можно рассматривать случайную
величину как функцию от элементарного события ![]() на пространстве
элементарных событий
на пространстве
элементарных событий ![]() .
.
В зависимости
от возможных значений все случайные величины можно разбить на два класса –
дискретные и непрерывные.
Дискретной назовём случайную величину, возможные значения
которой образуют или конечное множество, или счётное (бесконечное множество,
элементы которого можно пронумеровать).
Для задания
случайной величины недостаточно знать все её
возможные значения; две случайные величины могут иметь одинаковые
возможные значения, но принимать их с различными вероятностями (случайные
величины – оценки на экзамене у сильных и слабых студентов имеют одинаковые
возможные значения). Поэтому необходимо указать и возможные значения случайной
величины, и вероятности, с которыми она может их принять.
Назовём законом распределения дискретной случайной
величины правило, по которому каждому возможному значению ставится в соответствие
вероятность, с которой случайная величина может принять это значение.
Закон
распределения дискретной случайной величины может быть задан графически,
аналитически и таблично. В последнем случае задаётся таблица, где в одной
строке записаны все возможные значения, а в другой соответствующие им
вероятности.
Поскольку в
результате опыта случайная величина может принять одно и только одно из
возможных значений, то события, заключающиеся в том, что ![]() примет значения
примет значения ![]() образуют полную
группу (попарно несовместны и в сумме образуют достоверное событие). Отсюда
следует, что вероятность суммы этих событий равна единице
и мы приходим к важному соотношению
образуют полную
группу (попарно несовместны и в сумме образуют достоверное событие). Отсюда
следует, что вероятность суммы этих событий равна единице
и мы приходим к важному соотношению
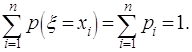 (2.1)
(2.1)
Замечание. Если множество возможных значений бесконечно и
счётно, то вместо
конечной суммы будет бесконечная – сумма ряда.
Пример 1.
Абитуриент сдаёт два вступительных экзамена: по математике
и физике. Составить закон распределения случайной величины ![]() , числа полученных пятёрок, если вероятность получения
пятёрки по математике равна 0.8, а по физике – 0.6.
, числа полученных пятёрок, если вероятность получения
пятёрки по математике равна 0.8, а по физике – 0.6.
Решение. Очевидно, возможные значения ![]() есть 0, 1, 2, причём,
есть 0, 1, 2, причём,
![]()
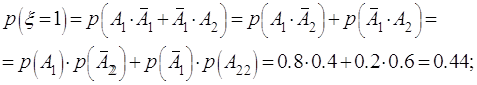
![]()
Здесь ![]() и
и ![]() – события, заключающиеся в том, что и
математика, и физика сданы на 5. При вычислении вероятностей использовались
несовместность слагаемых и независимость сомножителей. Сведём полученные
результаты в таблицу
– события, заключающиеся в том, что и
математика, и физика сданы на 5. При вычислении вероятностей использовались
несовместность слагаемых и независимость сомножителей. Сведём полученные
результаты в таблицу
|
|
0 |
1 |
2 |
|
|
0.08 |
0.44 |
0.48 |
Как легко проверить, условие нормировки (2.1)
выполняется.
Пример 2.
Вероятность появления события ![]() при одном испытании
равна
при одном испытании
равна ![]() . Составить закон распределения случайной величины
. Составить закон распределения случайной величины ![]() – числа испытаний, проведённых до первого
появления
– числа испытаний, проведённых до первого
появления ![]() .
.
Решение. Возможные значения ![]() – всецелые числа от 0 до
– всецелые числа от 0 до ![]() Предположим, что
Предположим, что ![]() и подсчитаем вероятность такого события. Очевидно, оно произойдёт, если
в первых
и подсчитаем вероятность такого события. Очевидно, оно произойдёт, если
в первых ![]() испытаниях произойдут события
испытаниях произойдут события ![]() , а в
, а в ![]() произойдёт событие
произойдёт событие ![]() . Отсюда искомая вероятность равна
. Отсюда искомая вероятность равна
![]()
здесь ![]() и мы
воспользовались независимостью сомножителей. Условие нормировки принимает вид
и мы
воспользовались независимостью сомножителей. Условие нормировки принимает вид
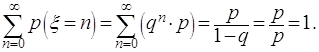
При вычислениях мы воспользовались формулой суммы членов
бесконечно убывающей прогрессии со знаменателем ![]() и первым (при
и первым (при ![]() ) членом, равным
) членом, равным ![]() .
.
Для задания
дискретной случайной величины можно ввести функцию распределения.
Назовём функцией распределения ![]() функцию,
равную вероятности того, что случайная величина
функцию,
равную вероятности того, что случайная величина ![]() примет значение, меньше
примет значение, меньше ![]() .
.
![]() (2.2)
(2.2)
При известном
законе распределения функция распределения дискретной случайной величины имеет
вид
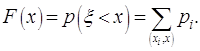 (2.3)
(2.3)
где ![]() означает, что
суммирование ведётся по всем индексам
означает, что
суммирование ведётся по всем индексам ![]() , для которых это неравенство выполняется. Функция
распределения
, для которых это неравенство выполняется. Функция
распределения ![]() дискретной случайной
величины
дискретной случайной
величины ![]() является
ступенчатой, сохраняющей постоянное значение на каждом интервале, не содержащем
точек
является
ступенчатой, сохраняющей постоянное значение на каждом интервале, не содержащем
точек ![]() и терпящих в этих
точках скачок, равный
и терпящих в этих
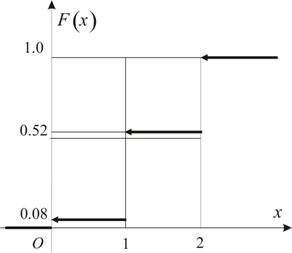
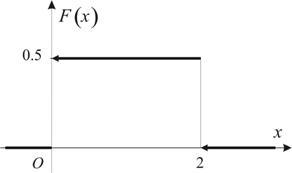
точках скачок, равный ![]() . Для примера 1 функция распределения и её график
представлены на Рис.2.1.
. Для примера 1 функция распределения и её график
представлены на Рис.2.1.
|
|
|
|
|
|
|
|
|
Рис.2.1 |
|
|
Пример 3.
Шарик (точка) бросается случайным образом на отрезок
длины ![]() так, что его положение
на отрезке равно возможно. Найдём вероятность
попадания брошенного шарика в заранее выбранную точку
так, что его положение
на отрезке равно возможно. Найдём вероятность
попадания брошенного шарика в заранее выбранную точку ![]() .
.
Решение. Определим вероятность попадания шарика на отрезок ![]() и устремим
и устремим ![]() к нулю. В
результате, согласно геометрической схеме, получаем
к нулю. В
результате, согласно геометрической схеме, получаем
![]()
Отсюда следует, что не всякое событие, вероятность
которого равна нулю, невозможное.
Поскольку
случайная величина ![]() , координата брошенной точки, в этом случае может принять
любое значение из интервала длины
, координата брошенной точки, в этом случае может принять
любое значение из интервала длины ![]() , то нельзя даже перечислить все её возможные значения и
вероятность того, что
, то нельзя даже перечислить все её возможные значения и
вероятность того, что ![]() примет
определённое значение
примет
определённое значение ![]() , равна нулю. Таким образом, определить закон распределения
так же, как и в дискретном случае, невозможно. Но и в этом случае функция
распределения сохраняет свой смысл:
, равна нулю. Таким образом, определить закон распределения
так же, как и в дискретном случае, невозможно. Но и в этом случае функция
распределения сохраняет свой смысл: ![]() При этом ясно, что
значения
При этом ясно, что
значения ![]() можно определить
для любого
можно определить
для любого ![]() . Будем в дальнейшем предполагать, что функция
. Будем в дальнейшем предполагать, что функция ![]() имеет производную
имеет производную ![]() , которая является непрерывной или кусочно-непрерывной
функцией на числовой оси. При этом, как
известно из курса математического анализа, справедливо равенство
, которая является непрерывной или кусочно-непрерывной
функцией на числовой оси. При этом, как
известно из курса математического анализа, справедливо равенство
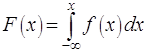 . Отсюда
. Отсюда ![]() .
(2.4)
.
(2.4)
В этом случае ![]() назовём непрерывно
распределённой функцией.
назовём непрерывно
распределённой функцией.
Пример 4.
Шарик бросается случайным образом на отрезок ![]() . Найти функцию распределения случайной величины –
координаты шарика.
. Найти функцию распределения случайной величины –
координаты шарика.
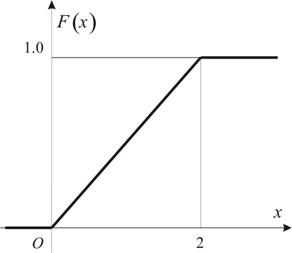
Решение. Разобьём ось ![]() на три интервала:
на три интервала: ![]() . Вид функции распределения и её график приведены на Рис.2.2,
причём, мы учитываем, что событие
. Вид функции распределения и её график приведены на Рис.2.2,
причём, мы учитываем, что событие ![]() на первом интервале
является невозможным, на втором, согласно геометрической схеме, имеет
вероятность
на первом интервале
является невозможным, на втором, согласно геометрической схеме, имеет
вероятность ![]() , а на третьем является достоверным.
, а на третьем является достоверным.
|
|
|
|
|
|
|
|
|
Рис.2.2 |
|
|
Рассмотренные
примеры показывают, что функция распределения имеет ряд свойств, справедливых и
в общем случае.
Функция
распределения ![]() определена на всей
числовой оси и
определена на всей
числовой оси и
![]() .
(2.5)
.
(2.5)
![]() – неубывающая функция, то есть для
– неубывающая функция, то есть для ![]()
![]() (2.6)
(2.6)
Действительно, событие
![]() включает событие
включает событие ![]() и поэтому
и поэтому
![]()
![]() (2.7)
(2.7)
Событие ![]() невозможно и его
вероятность равна нулю, а событие
невозможно и его
вероятность равна нулю, а событие ![]() достоверное и его
вероятность равна единице.
достоверное и его
вероятность равна единице.
Вероятность
попадания случайной величины в интервал ![]() равна приращению
функции распределения на этом интервале:
равна приращению
функции распределения на этом интервале:
![]() (2.8)
(2.8)
Действительно, пусть ![]() – событие,
заключающееся в том, что
– событие,
заключающееся в том, что ![]() а
а ![]() и
и ![]() – в том, что соответственно
– в том, что соответственно ![]() и
и ![]() . Пользуясь определением функции распределения и
несовместностью событий
. Пользуясь определением функции распределения и
несовместностью событий ![]() и
и ![]() , получаем:
, получаем:
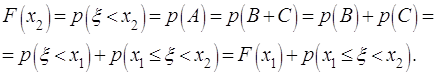
Отсюда следует справедливость (2.8).
Плотность вероятности
Рассмотрим
некоторую непрерывно распределённую случайную величину ![]() . Согласно предыдущему, функция распределения имеет вид:
. Согласно предыдущему, функция распределения имеет вид:
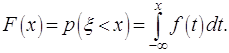
Функцию
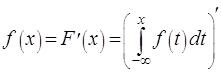 . (2.9)
. (2.9)
принято называть плотностью распределения вероятностей
или плотностью вероятностей. Таким образом,
плотность вероятности некоторой случайной величины равна
производной от её функции распределения.
Свойства плотности вероятности
Плотность вероятности – неотрицательная
функция. Это свойство следует из того, что функция распределения
– не убывающая и, следовательно, её производная больше или равна нулю.
Вероятность попадания случайной величины
в интервал ![]() равна интегралу от плотности
вероятности по этому интервалу.
равна интегралу от плотности
вероятности по этому интервалу.
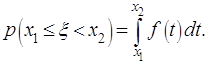 (2.10)
(2.10)
Действительно, по свойству функции распределения
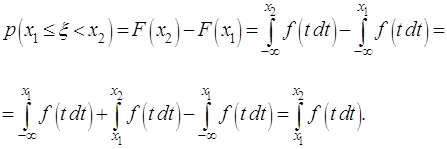 (2.11)
(2.11)
Определённый интеграл от плотности
вероятности по всей числовой оси равен единице. Это утверждение следует из
того, что
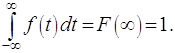 (2.12)
(2.12)
Подводя
итоги, отметим, что плотность вероятности – неотрицательная функция,
удовлетворяющая условию нормировки (1.12), которое означает, что площадь
фигуры, ограниченной графиком ![]() и осью
и осью ![]() , равна единице. Очевидно, любая неотрицательная функция,
удовлетворяющая (1.12), может рассматриваться как плотность вероятности
некоторой случайной величины.
, равна единице. Очевидно, любая неотрицательная функция,
удовлетворяющая (1.12), может рассматриваться как плотность вероятности
некоторой случайной величины.
Пример 5.
Найдём плотность вероятности случайной величины,
рассмотренной в примере 4, и построим её график (Рис.2.3).
|
|
|
|
|
|
|
|
|
Рис.2.3 |
|
|