1.6. Асимптотические формулы
Применение формулы Бернулли при больших значениях ![]() приводит к произведению
очень больших
приводит к произведению
очень больших ![]() и очень малых чисел (
и очень малых чисел (![]() и
и ![]() ), что плохо с вычислительной точки зрения, поэтому
приходится пользоваться приближёнными, асимптотическими формулами.
), что плохо с вычислительной точки зрения, поэтому
приходится пользоваться приближёнными, асимптотическими формулами.
Формула Пуассона
Рассмотрим ситуацию, в которой число испытаний ![]() в схеме Бернулли неограниченно
увеличивается, а вероятность наступления события
в схеме Бернулли неограниченно
увеличивается, а вероятность наступления события ![]() в каждом испытании
стремится к нулю таким образом, что произведение
в каждом испытании
стремится к нулю таким образом, что произведение ![]() остаётся величиной
постоянной, которую обозначим
остаётся величиной
постоянной, которую обозначим ![]() . В этом случае имеет место соотношение:
. В этом случае имеет место соотношение:
![]() (1.19)
(1.19)
Доказательство. По формуле Бернулли
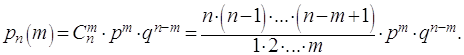
Воспользуемся тем, что по условию ![]() или
или ![]() и
и ![]() Формула Бернулли
принимает вид:
Формула Бернулли
принимает вид:
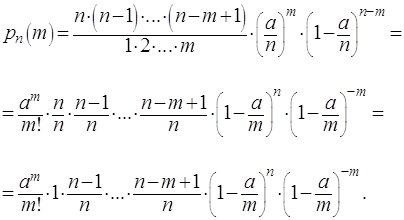
Так как ![]() и
и ![]() фиксированы, а
фиксированы, а ![]() стремится к
бесконечности, то множители
стремится к
бесконечности, то множители 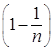 ; … ;
; … ; 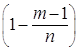 и
и 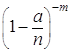 стремятся к единице, а
множитель
стремятся к единице, а
множитель 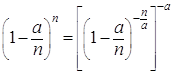 стремится к
стремится к ![]() , то
, то
![]()
Полученное выражение называется Пуассоновским приближением формулы Бернулли.
Эта формула даёт хорошее приближение при достаточно большом ![]() и малом
и малом ![]() (например,
(например, ![]() и
и ![]() ).
).
Вероятность события, заключающегося в том, что ![]() появится не более
появится не более ![]() раз, очевидно,
вычисляется по формуле
раз, очевидно,
вычисляется по формуле
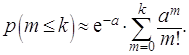 (1.20)
(1.20)
При проведении расчётов можно пользоваться тем, что обе формулы табулированы
(Таблицы 1 и 2).
Локальная и интегральная формулы Муавра-Лапласа
При
достаточно большом n и не слишком малых p и q формула Пуассона
уже даёт значительную погрешность и применяется другое приближение – формула Муавра - Лапласа, которую можно получить из
формулы Бернулли, совершая предельный переход и применяя формулу Стирлинга для
вычисления ![]()
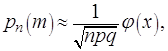 где
где 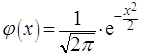 и
и ![]() (1.21)
(1.21)
Эта формула также табулирована
(Таблица 3), причём в силу чётности функции ![]() , таблица её значений составлена только для
, таблица её значений составлена только для
![]()
Если при сохранении условий предыдущего пункта нас интересует вероятность
того, что при ![]() испытаниях событие
испытаниях событие ![]() появляется не менее
появляется не менее ![]() и не более
и не более ![]() раз, то формула (1.18)
с учётом предельного перехода превращается в интегральную формулу
Муавра-Лапласа:
раз, то формула (1.18)
с учётом предельного перехода превращается в интегральную формулу
Муавра-Лапласа:
![]()
где
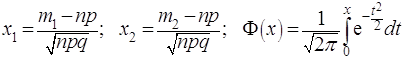
и сумма превращается в интеграл. Функция
![]() – интеграл от
– интеграл от ![]() – называется функцией Лапласа и представляет собой не
выражающийся через элементарные функции интеграл. Поскольку функция Лапласа
нечётная (
– называется функцией Лапласа и представляет собой не
выражающийся через элементарные функции интеграл. Поскольку функция Лапласа
нечётная (![]() ) и быстро приближается к своему асимптотическому значению
0.5, то таблица её значений (Таблица 4) составлена для
) и быстро приближается к своему асимптотическому значению
0.5, то таблица её значений (Таблица 4) составлена для
![]() . Для больших значений аргумента с
большой точностью можно принять
. Для больших значений аргумента с
большой точностью можно принять ![]() .
.
Пример 16.
При установившемся технологическом
процессе ЖБК выпускает 80% всех изделий первым сортом. Найти вероятность, что : из 100 поставленных первосортных будет ровно 75, не менее
75.
Решение. Поскольку n = 100 велико,
p = 0,8 и q = 0,2 не малы, применяем локальную и затем
интегральную формулы Муавра-Лапласа
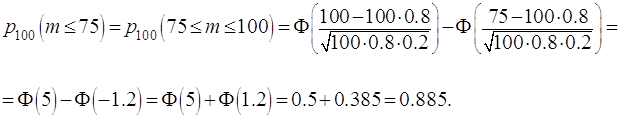
Пример 17.
Известно, что при транспортировке и
разгрузке керамической отделочной плитки повреждается 2.5% товара. Найти вероятность того, что в партии из200
плиток повреждёнными окажутся ровно 4; не более 6.
Решение. Поскольку вероятность ![]() повреждения плитки
мала,
повреждения плитки
мала, ![]() велико и
велико и ![]() , можно воспользоваться формулами Пуассона (1.19); (1.20),
применяя таблицы 1 и 2:
, можно воспользоваться формулами Пуассона (1.19); (1.20),
применяя таблицы 1 и 2:
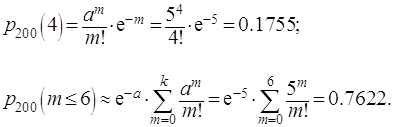
Пример 18.
Известно, что 30% призывников имеют
27 размер обуви. Сколько пар обуви надо иметь на складе воинской части, чтобы с
вероятностью Ро = 0,9 были обеспечены все такие призывники, если в
часть прибыло 200 новобранцев ?
Решение. Очевидно, имеет место схема
Бернулли : подбор пары обуви каждому призывнику - одно из 200 испытаний, причём
вероятность того, что ему потребуется обувь 27 размера равна ![]() (
(![]() ). Пусто на складе имеется
). Пусто на складе имеется ![]() , где
, где ![]() пока не известно.
Требуется подобрать такое
пока не известно.
Требуется подобрать такое ![]() , чтобы
, чтобы ![]() . Поскольку
. Поскольку ![]() велико, а
велико, а ![]() и
и ![]() не малы,
применяем интегральную формул Муавра-Лапласа
не малы,
применяем интегральную формул Муавра-Лапласа
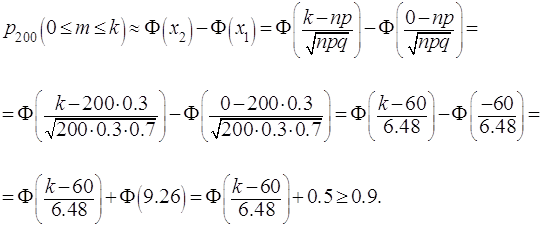
Отсюда
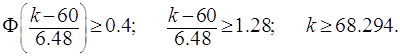
То есть на складе достаточно иметь
69 пар обуви такого размера, чтобы с вероятностью 0,9 обеспечить спрос.
Пример 19.
Вероятность того, что зашедший в
ресторан посетитель сделает заказ равна 0.8.
Определить вероятность того, что из 100 зашедших ровно
75 сделают заказ: не менее 75.
Решение. Поскольку ![]() велико,
велико, ![]() и
и ![]() не малы, применяем локальную
и затем интегральную формулы Муавра-Лапласа
не малы, применяем локальную
и затем интегральную формулы Муавра-Лапласа
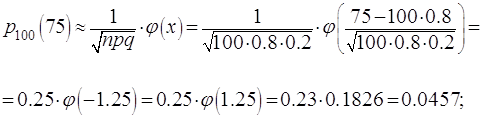
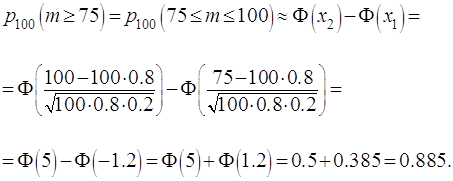
Простейший стационарный (Пуассоновский) поток событий
Пусть на некоторой прямой расположены точки так, что в
среднем на единицу длины приходится ![]() точек.
Последнее не следует понимать так, что на любой единичный отрезок приходится
ровно
точек.
Последнее не следует понимать так, что на любой единичный отрезок приходится
ровно ![]() точек, но если взять
достаточно большой по длине отрезок
точек, но если взять
достаточно большой по длине отрезок ![]() и разделить число
точек
и разделить число
точек ![]() , оказавшихся в нём, на его длину, то отношение
, оказавшихся в нём, на его длину, то отношение ![]() при неограниченном
увеличении
при неограниченном
увеличении ![]() будет как угодно мало
отличаться от
будет как угодно мало
отличаться от ![]() , то есть
, то есть ![]() играет роль средней
плотности.
играет роль средней
плотности.
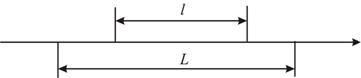
Вероятность того, что одна точка окажется на отрезке длины l , зависит только от его длины и не зависит от его
расположения на прямой. Точки распределяются на прямой независимо друг от друга.
|
|
|
|
|
|
|
Рис.1.7 |
Определим теперь вероятность того, что ровно ![]() точек окажется на
отрезке длиной
точек окажется на
отрезке длиной ![]() . Для этого введём в рассмотрение отрезок
. Для этого введём в рассмотрение отрезок ![]() , целиком включающий в себя отрезок
, целиком включающий в себя отрезок ![]() , причём,
, причём, ![]() (Рис.1.7). Согласно
принятым допущениям на отрезке
(Рис.1.7). Согласно
принятым допущениям на отрезке ![]() расположено
расположено ![]() точек, причём каждая
из них может оказаться в любом месте отрезка
точек, причём каждая
из них может оказаться в любом месте отрезка ![]() и все эти положения равно возможны.
Вероятность того, что одна из этих точек окажется на отрезке
и все эти положения равно возможны.
Вероятность того, что одна из этих точек окажется на отрезке ![]() , согласно справедливой в этом случае геометрической схеме,
равна
, согласно справедливой в этом случае геометрической схеме,
равна ![]() и не зависит от того,
какая из этих точек первая, вторая и т.д.
и не зависит от того,
какая из этих точек первая, вторая и т.д.
В результате мы пришли к схеме Бернулли (производится ![]() испытаний, в каждом из которых мы следим за одной точкой, и
любая из них с вероятностью
испытаний, в каждом из которых мы следим за одной точкой, и
любая из них с вероятностью ![]() может оказаться на
отрезке
может оказаться на
отрезке ![]() ). Поэтому вероятность
того, что ровно
). Поэтому вероятность
того, что ровно ![]() точек из
точек из ![]() окажется на
отрезке
окажется на
отрезке ![]() , определяется по формуле Бернулли
, определяется по формуле Бернулли ![]() где
где ![]() ;
; ![]() . При неограниченном увеличении
. При неограниченном увеличении ![]() , длина отрезка стремится к бесконечности, а
, длина отрезка стремится к бесконечности, а ![]() к нулю, но при этом
величина
к нулю, но при этом
величина ![]() остаётся постоянной.
Следовательно, можно применять формулу Пуассона, которая в данном случае
является точной, а не асимптотической:
остаётся постоянной.
Следовательно, можно применять формулу Пуассона, которая в данном случае
является точной, а не асимптотической:
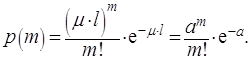 (1.22)
(1.22)
Если нас интересует вероятность того, что на отрезке ![]() окажется не менее
окажется не менее ![]() точек, то применяется
формула
точек, то применяется
формула
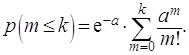 (1.23)
(1.23)
Разумеется, вместо отрезка на прямой можно рассматривать плоскость и некоторую
её область, трёхмерный случай или вообще случай любого числа измерений, а также
временной отрезок. В каждом из этих случаев ![]() – среднее число элементов, приходящихся на рассматриваемую
область.
– среднее число элементов, приходящихся на рассматриваемую
область.
Напомним, что формулы (1.22) и (1.23) табулированы (таблицы 1 и 2).
Пример 20.
На факультете учатся 500 студентов.
Найти вероятность того, что первое сентября является днём рождения: трёх
студентов, не менее трёх.
Решение. Пусть событие А -
случайно выбранный студент родился первого сентября, тогда ![]() . В результате пришли к схеме Бернулли, где число
испытаний n = 500 велико, а p мало (события
редкие) и при np = 1,37 <
10, поэтому применяем формулы Пуассона
. В результате пришли к схеме Бернулли, где число
испытаний n = 500 велико, а p мало (события
редкие) и при np = 1,37 <
10, поэтому применяем формулы Пуассона
![]()
Здесь мы воспользовались таблицами 1
и 2 и во втором случае для этого перешли к противоположному событию.
Пример 21.
Известно, что в среднем за месяц (30
суток) в районной сети водоснабжения возникает 90 ситуаций, требующих
оперативного вмешательства аварийной службы. На сколько вызовов в сутки должна
быть рассчитана эта служба, чтобы с вероятностью ![]() она могла
удовлетворить все поступающие за эти сутки заявки?
она могла
удовлетворить все поступающие за эти сутки заявки?
Решение. Предположим, что аварийная служба
рассчитана на ![]() заявок в сутки, где
заявок в сутки, где ![]() пока не известно.
Пусть m - число поступивших за сутки. Тогда
пока не известно.
Пусть m - число поступивших за сутки. Тогда
![]() найдём из условия
найдём из условия ![]() . Поскольку поток заявок представляет собой простейший,
стационарный (Пуассоновский) поток событий, то можно применить формулу
Пуассона
. Поскольку поток заявок представляет собой простейший,
стационарный (Пуассоновский) поток событий, то можно применить формулу
Пуассона ![]() , где
, где ![]() среднее число заявок
за сутки. Для определения
среднее число заявок
за сутки. Для определения ![]() воспользуемся таблицей
2 при
воспользуемся таблицей
2 при ![]() , подбирая
, подбирая ![]() таким
образом, чтобы искомая вероятность была не меньше, чем
таким
образом, чтобы искомая вероятность была не меньше, чем ![]() . В результате получим
. В результате получим
![]() , то есть аварийная служба должна быть рассчитана на 5 заявок
в сутки.
, то есть аварийная служба должна быть рассчитана на 5 заявок
в сутки.